問題文より「上面:側面の空気密度の比が4:5」であるのに、上面を通る鉛直流の風速が5Vになるのはどうしてですか?
上面から出ていくので、上面の密度の比の4Vだと考えてしまいます
(問題)
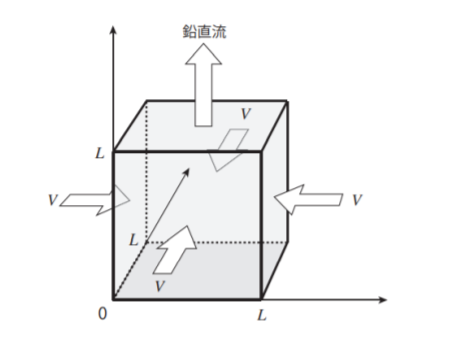
図のように,大気中に一辺の長さが L の立方体の領域があり,その四つの側面を通して密度ρの
空気が面に垂直な一定の風速 V で内部に吹きこんでいる。このとき,単位時間に四つの側面を通
して立方体に流入する空気の質量は(a)で表される。また,立方体内の大気の質量は時間的に変
化せず底面を通した空気の流入・流出はないとすれば,立方体の上面を通る鉛直流の風速は(b)
となる。ただし,立方体の上面,側面,底面における平均的な空気密度の比は 4:5:6 であるとし,
鉛直流の符号は上向きを正とする。

(問題解答)
立方体に流入する面は、側面(4面)のみです。1つの面(面積はL×2=2Lとする)には、速度Vで
密度ρの空気が吹き込むので、その流入量は、V×ρ×L2です。それが 4 面あるので、4×V×ρ
×2L となり、(a)は③か④となります。
一方、流出は上面のみです。ここで注意することは、但し書きにある「立方体の上面、側面、底面
における平均的な空気密度の比は4:5:6」という文言です。側面から流入した風速の合計は4×
Vですが、上面と側面の密度の比は4:5なので、上面を通る鉛直流の速度は5×Vとなります。よ
って、正解は④となります。
(さらに解説)
問題文より
上面:側面の空気密度の比=4:5
風が入ってくるのは側面のみ
⇒4V
風が出ていくのは上面のみ
答えは5Vなのはなぜなのか…
問題を考えるとき
側面から入ってくる風の量と上面から出ていく風の量は
同じにならなければいけません。
例えば掃除機で、吸い込む風の量と、排気の量が同じじゃないと
掃除機が調子悪いか、壊れるのと同じです
上面:側面の密度の比が4:5だから
上面の風は「4V」と考えたようですが…
側面の風速が「5V」なら比の値から、わからんこともないです(まちがいですが…)
上面の風が4V、側面の風も4V。
比例させるなら矛盾しています。密度や比が全く反映されないことになります
ここで密度の意味を考えましょう
密度=単位体積あたりの重さです
例えば同じ大きさの箱があるとして
密度が4:5だとすると
同じ大きさのパンがあるとして
密度が4:5とすると
4のほうが「少しスカスカ」で軽いはずです
同じ重さにしようとすると
4のほうのパンを少し多くしないといけませんよね?
(フランスパンのような同じ形のパンを考えたとき
スカスカの方のパンの長さを長くすれば重さがおなじになるはずです)
密度は「単位体積あたりの重さ」と言う話をしました
密度(ρ)と体積(V)と重さ(質量:M)の関係は
密度=質量÷体積
ρ=M/V です
さて本題に入りましょう
①
側面から入っていく風の量(体積)と
上面から出ていく風の量(体積)が同じじゃないといけません
(風は空気なので重さは同じ この問題では計算上無視できます
無視できる場合は「1」と考えておけばいいです)
②
また問題文より立方体なので
そのため、側面と上面の入っていくところの面積は同じです
立方体や直方体の体積は「面積×高さ」
(この問題では上面の面積と側面積が同じです)
この「高さ」のところを「風の速さ」と考えるのです
この①と②を先程の式にいれこむと
密度=重さ÷体積
=重さ÷(“上面面積or側面積”×高さ)
③
重さと面積はこの問題は同じなので計算上、無視できるので
仮に1としておきます
また高さは「風速」です
密度=1/風速
また
風速V=1/密度
⇒風速と密度は単純に反比例の関係なのです
④ということで
上面:側面の密度比が4:5でした
逆に
上面:側面の風速比は5:4の反対になれば合うわけです
上面=□ 側面=4V
5:4=□:4V
□=5V
こういう解き方です
もう一つの考え方です。
側面から入る風の量は
側面の面積×高さ(風速)
上面から出ていく風の量は
上面の面積×高さ(風速)
側面と上面の面積が同じなので無視して風速だけを考える
この問題で
風速と密度の関係は
風速=1/密度でした
また側面から入る風速
4Vなので
4V=1/5
上面から入る風速□は
□=1/4
これが同じになればいいわけです
□=5Vです
実はダウンバーストなど風の問題で
側面積(などの面積)×高さで風の量を出すときに
高さを風速でみなす問題、結構出ます