ここでは、気体に関する熱力学の第一法則について学びます。

文系さんでも、理科の授業を忘れてしまった方でも、大丈夫。
私がわかりやすく説明しますからね!
熱力学第一法則は、一見むずかしそうですが、実は「エネルギーの収支表」をまとめただけのものです。
ただし、分野によって“仕事 W をどちら向きでプラスにするか”が違うため、式が 2 通り存在します。
この記事では、気象の分野で使う書き方と、工学系の書き方を同じ現象で比較しながら、
「なぜ式が違っても同じ結果になるのか」が自然に理解できるように解説します。
熱力学第一法則の基本イメージ
まず押さえておきたいのは、
内部エネルギー ΔU は、
Q(熱の出入り)+ W(仕事の出入り) で決まる。
というシンプルな事実だけです。
気体を「エネルギーの貯金箱」だと思うとわかりやすく
- エネルギーが外から入ってくればプラス
- エネルギーが外に出ていけばマイナス
という感覚で判断できます。

U:内部エネルギー
内部エネルギー U は、その気体が“もともと持っているエネルギーの総量”を表します。
より具体的には──
- 分子がどれくらい速く動いているか(運動エネルギー)
- 分子同士がどれくらい振動したり回転したりしているか
- 状態の乱れ(分子の自由度)
これらを全部ひっくるめた「分子レベルのエネルギーの合計値」です。
ポイント
内部エネルギーの増減は、温度の変化そのものと対応します。
- U が増える → 温度が上がる
- U が減る → 温度が下がる
つまり ΔU は「気体がどれくらい温まったか・冷えたか」を表す量だと考えると直感的です。
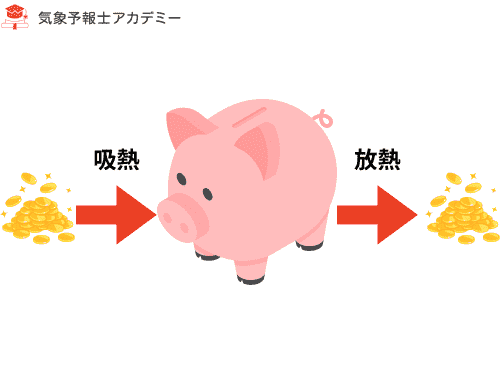
Q:熱量
Q は、“熱として”外部とやり取りしたエネルギーです。
“熱”というと何となく「温かい・冷たい」の感覚で捉えがちですが、物理的には
温度差によって自動的に移動するエネルギー
のことを言います。
Q の意味
- Q > 0:気体が外から熱をもらった(吸熱)
- Q < 0:気体が外へ熱を出した(放熱)
ストーブで温められる、太陽で暖まる、氷で冷やされる──
こうした「外との熱のやり取り」はすべて Q の変化として扱います。
注意
Q は「温度を変える原因のひとつ」ですが、温度そのものではありません。
W:仕事
W は、力によって行われるエネルギーのやり取りです。
気体の世界では特に、
気体が押された・押し返したときに発生するエネルギーの交換
のことを指します。
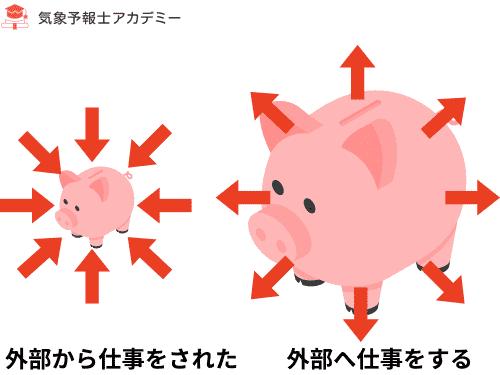
仕事のイメージ
気体は押されると縮み、膨らむと外へ押し返します。
このとき、
- 押されて縮められる → 気体は「外部から仕事をされた」
- 膨張して外へ押す → 気体は「外部へ仕事をする」
という関係があります。
符号の違い
これは分野によって定義が異なります。
気象・物理の定義
- 圧縮される(外から押される) → W > 0
- 膨張する(外に押し返す) → W < 0
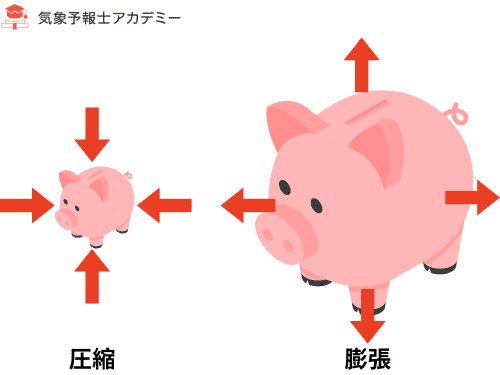
工学系の定義
- 膨張して外に押す → W > 0
- 圧縮される → W < 0
どちらも間違いではなく、どちらをプラスにするかの約束が違うだけです。
<Q・W・U> 3つのの量の関係が「熱力学第一法則」
- Q(熱としての出入り)
- W(仕事としての出入り)
- U(気体自身のエネルギーそのもの)
この 3 つがどう変わったかを表すのが熱力学第一法則で、形式としては以下のようになります。
気象・物理系の形式
ΔU = Q + W
(外部 → 系 のエネルギー流入がプラス)
工学系の形式
ΔU = Q − W
(系 → 外部 への仕事がプラス)
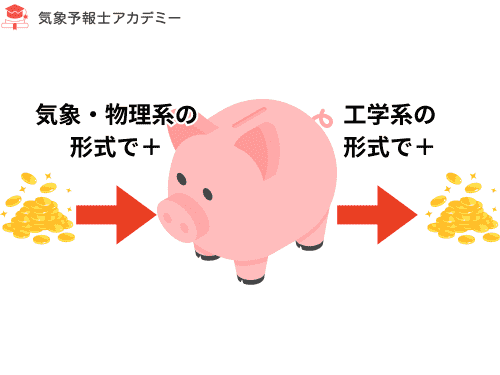
定義は違っても、物理的な世界はひとつなので、
同じ現象を計算すれば ΔU は必ず一致します。
気象で使う書き方:ΔU = Q + W
気象や物理の教科書で一般的な定義がこちらです。
ΔU = Q + W
(外部 → 系 へのエネルギーをプラス)
Q(熱量)の符号
- Q > 0:外から熱をもらう(吸熱)
- Q < 0:外へ熱を出す(放熱)

W(仕事)の符号
- W > 0:外部から気体が押される(圧縮)=気体は仕事を“される”
- W < 0:気体が外へ押し返す(膨張)=気体が仕事を“する”

つまりこの書き方は、
外から入ってくるエネルギーをプラスにする解釈です。
例えば・・・外とのエネルギーの出入りがないとすると、Qの値は変わらないということ(一定)になりますね。
この状態で、空気の体積を大きくすると(膨張させると)、 W は減るので、内部エネルギーU も減少します。
逆に空気の体積を小さくすると(圧縮させると)、 W は増えるので、内部エネルギーU も増加します。
工学で使う書き方:ΔU = Q − W
一方、機械工学・熱機関分野では、仕事の向きを反対で定義します。
ΔU = Q − W
(系 → 外部 への仕事をプラス)
こちらは、蒸気機関やエンジンのように、
「どれだけ外へ仕事を取り出せたか」を重視する文化に合った定義です。
この体系ではどうなるか(この部分が異なる)
- 膨張して外に仕事する → W > 0(プラス)
- 圧縮されて外から仕事を受ける → W < 0(マイナス)
つまり、外へ仕事を出した分だけ内部エネルギーが減るという考え方です。
例えば・・・外とのエネルギーの出入りがないとすると、Qの値は変わらないということ(一定)になりますね。
この状態で、空気の体積を大きくすると(膨張させると)、 W は増えるので、内部エネルギーU は減少します。
逆に空気の体積を小さくすると(圧縮させると)、 W は減るので、内部エネルギーU も増加します。
ややこしいですね・・・次でスッキリまとめてしまいましょう!
同じ現象を両符号系で書くとどうなる?

さて話を進めますよ。
同じ物理現象でも、式が違うと計算がズレそうに見えるかもしれません。
しかし実際には──
符号の扱いが違うだけで、内部エネルギー ΔU の値は必ず一致します。
そのことを確認するため、例題で比較してみましょう。
例題:吸熱 + 膨張 の典型パターン
外部から 50 J の熱を受け取り(吸熱)、
気体が外へ向けて 20 J の仕事をした(膨張)。
内部エネルギー ΔU はどうなるか?
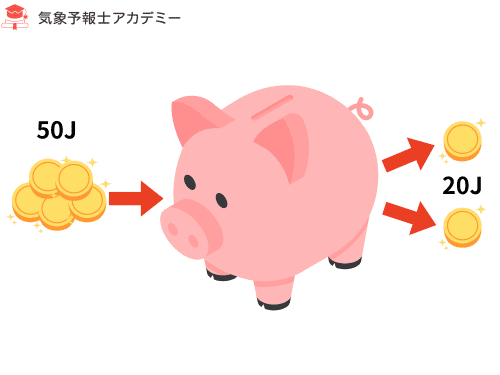
この「吸熱+膨張」は、符号の違いが最もよく表れる代表的なパターンです。
両体系の比較表(この章が最重要)
| 式の体系 | W の定義 | 今回の W の符号 | 使う式 | ΔU の計算 | ΔU の結論 |
|---|---|---|---|---|---|
| 気象・物理系 | 外部 → 系 の仕事がプラス | 膨張 → W = −20 | ΔU = Q + W | ΔU = +50 + (−20) | +30 J |
| 工学系 | 系 → 外部 の仕事がプラス | 膨張 → W = +20 | ΔU = Q − W | ΔU = +50 − 20 | +30 J |
★ ここから言えること
どの体系で計算しても
ΔU = +30 J
という物理的な結果は必ず一致します。
式の違いは「プラスをどちらに取るか」という記号上の文化の違いにすぎず
実際の物理現象は何も変わりません。
直感的まとめ
- “外からもらうもの”をプラスにする → ΔU = Q + W
- “外へ出す仕事”をプラスにする → ΔU = Q − W
- どちらを使っても、ΔU は必ず一致する

熱力学第一法則は、形式が 2 種類あってややこしく見えますが、本質は「エネルギーの出入りの帳簿をどう書くか」だけの違いです。
符号の約束事さえ整理してしまえば、むしろ一気に理解しやすくなるはずです。
これで熱力学第一法則について、一通り説明は終わりです。
最後にあなたが熱力学の第一法則について、しっかり理解できているか確認するために、練習問題を解いてみましょう!
練習問題
熱力学第一法則を思い出しながら、以下のクイズに挑戦してみましょう!
問題1
外部から熱が加えられることなく(断熱)、気体を圧縮した場合、気体の内部エネルギーはどのように変化しますか?
①増加する
②減少する
③変化なし
答え:①増加する
【解説】
熱が加えられないため、Q = 0 となります。また、気体を圧縮したということは、外部から仕事をされたということなので、W はプラスになります。熱力学第一法則 ΔU = Q + W にあてはめると、ΔU = 0 + W となり、ΔUはプラスになります。
問題2
気体が外部から 50 J の熱を受け取り、同時に外部に 20 J の仕事をしました。このとき、気体の内部エネルギーはどれだけ変化しますか?
30 J 増加する
【解説】
外部から熱を受け取ったので、Q = + 50 J となります。
外部に仕事をしたので、W = − 20 J となります。
熱力学第一法則 ΔU = Q + W にあてはめると、ΔU = 50 J + ( – 20 J ) = 30 J となります。
問題3
ある気体が、外部から 30 J の仕事をされ、その内部エネルギーが 10 J 増加しました。このとき、外部から気体に加えられた熱量はどれだけですか?
– 20 J( 20 J の熱を放出した)
【解説】
外部から仕事をされたので、W = + 30 J となります。
内部エネルギーが 10 J 増加したので、ΔU = + 10 Jとなります。
熱力学第一法則 ΔU = Q + W にあてはめると
10 J = Q + 30 Jとなり
Q = 10 J − 30 J = −20 J となります。
マイナスなので、気体は熱を放出したことになります。
さいごに
熱力学第一法則についての勉強、お疲れ様でした!
今回の記事で、熱力学の基礎は理解できたかもしれません。
しかし、本番の試験では、複雑な問題が組み合わさって出題されます。
独学では、一つひとつの公式は理解できても、それらを組み合わせて応用する力や、見慣れない問題に対応する力を身につけるのは難しいものです。
その壁を乗り越えるために、私たちの講座があります。
私たちは、公式をただ暗記するのではなく、その「なぜ」を徹底的に解説し、どんな問題にも対応できる応用力を養います。
経験豊富な講師があなたの疑問に一つひとつ丁寧にお答えし、あなたが一人で悩む時間を、合格へと繋がる貴重な学習時間に変えます。
独学での勉強に行き詰まりを感じている方、効率的な学習法を探している方は、ぜひ一度、私たちの無料相談をご利用ください。
あなたが未来の気象予報士になる日を、心から応援しています。
「気象予報士の資格は取りたいけど、どのように勉強すれば良いのかわからない」
「テキストを買ってみたけれど、わからないことだらけ…」
「一人で受験勉強をする自信がない」
などなど、一人で悩んでいませんか?
当講座では、この記事で解説したような専門的な内容も、初学者の方が基礎から着実に理解できるようカリキュラムを組んでいます。
AIチューターが即座に疑問を解消し、担当講師がマンツーマンで、あなたの『わからない』を徹底的にサポート。
勉強内容だけでなく、あなたに最適な学習計画も一緒に考え、独学では難しい最新の予報技術も効率的に習得できます。
今すぐ、気象予報士合格への第一歩を踏み出しませんか?
▶︎【合格ロードマップ公開!】気象予報士アカデミーで学ぶ最短合格への3ステップ
LINEで友達登録すると、3分でわかる気象予報士合格ポイント動画をプレゼント!
マンツーマンの受講相談で、あなたの疑問や不安を解消しましょう!!!
\ 講座へのご質問はお気軽に! /